As I watched Suni Lee leap through the air, I only had two questions in my mind. “How did she manage to jump so high while pivoting? Why are a lot of gymnasts relatively short?” The answer to the first question is probably because of consistent training and physics. In myriads of sports, especially for vital movements, physics is not a shocking element.
When I found the answer to the height question, I must say that it is surprising. The average height of elite female gymnasts has shrunk from about 5” 3 on average to about 4” 9 in the last 25 years. Their petite figures complement the sport quite excellently because of better moments of inertia. What does this mean? Moment of inertia refers to a body’s resistance to rotation, a measurement of both the amount of mass and how far it is from the axis of rotation. When an object has a higher moment of inertia, it will be more difficult to rotate it. Hence, by being smaller and doing deliberate movements (such as tucking the hands closer to the body), a lot of the mass is clustered around the body’s axis of rotation. Hence, shorter gymnasts can have a lower moment of inertia, making it much easier for them to pivot pretty rapidly.
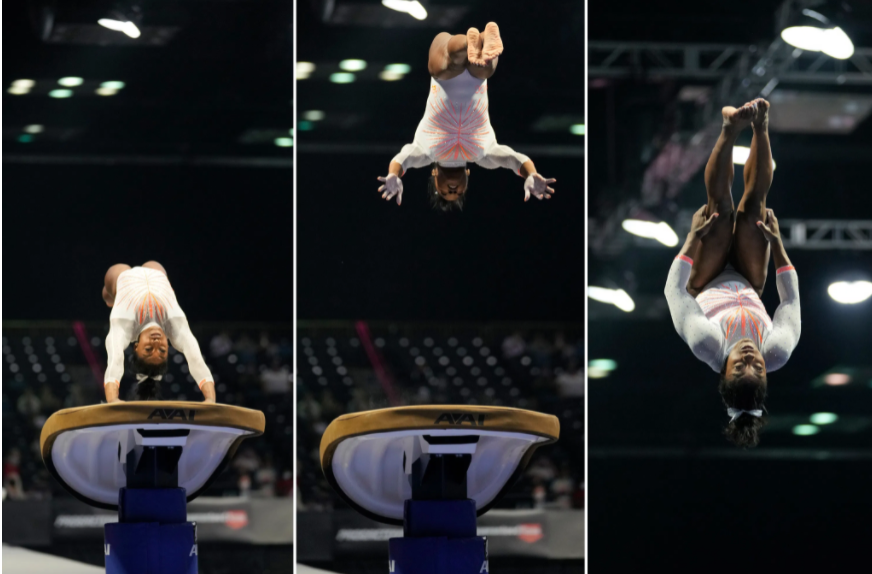
Now, let’s look at another movement that Simone Biles did: the Yurchenko double pike. For her Olympics routine, she starts by running towards the vault table. Then, execute two round-offs, a technique quite similar to cartwheels. At the start, notice how her body is in a nearly straight position before bending into the pike after she bounces off the table. Because of the change in the mass distribution around the axis of rotation, her moment of inertia also changes. Science journalist Rhett Allain calculated that the ratio of moments between the pike and straight positions is 2:3. A possible factor is that during the pike position, her angular velocity (how fast a body rotates on an axis) is 15.49 rad/s, whereas, in a straight position, it is approximately 6.27 rad/s. Do take note that her angular velocity in the pike position is more than twice that of the straight position, allowing her to properly land on her feet.
With rigorous training, gymnasts can properly implement these laws of physics into their movements (even if they do not do it consciously) and complete successful rotations mid-air.
Resources
Comments